Python ile EKOK ve EBOB Bulma
Bu yazımızda, Python kullanarak EKOK(En küçük ortak kat) ve EBOB(En büyük ortak bölen) bulan program oluşturacağız. Oluşturduğumuz program, veri olarak girdiğimiz dizinin bütün elemanları arasında hesaplama yapacak. Python’da bulunan modüllerdeki hazır fonksiyonlar ile kolay bir şekilde EKOK veya EBOB hesaplayabiliyoruz ancak modüllere bağlılığı azaltmak ve programlama bilgimizi geliştirmek için kendimiz EKOK ve EBOB bulan bir program oluşturacağız. Kodlamaya geçelim:
EKOK:
1
2
3
4
5
6
7
8
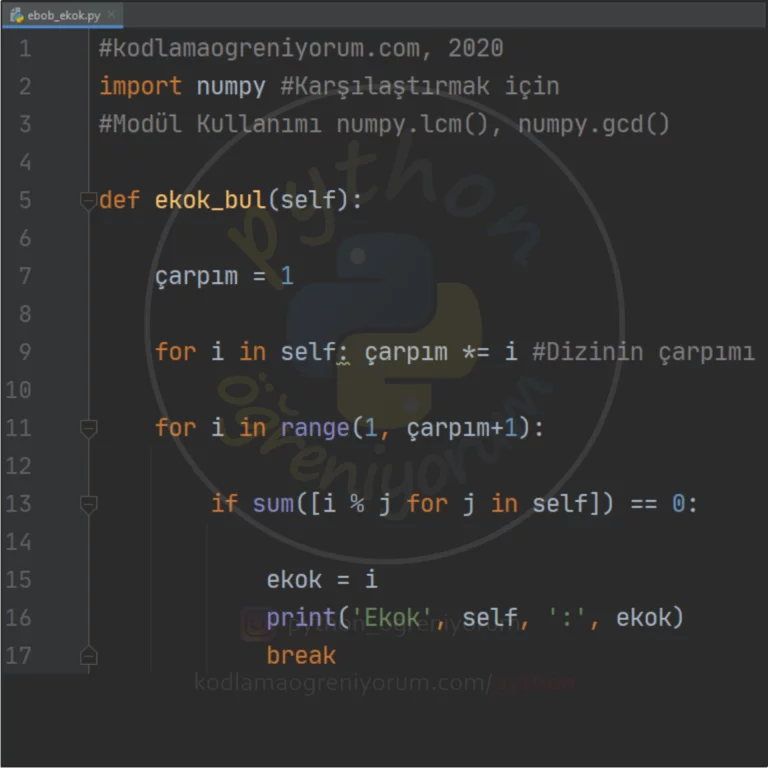
def ekok_bul(self):
çarpım = 1
for i in self: çarpım *= i #Dizinin çarpımı
for i in range(1, çarpım+1):
if sum([i % j for j in self]) == 0:
ekok = i
print('Ekok', self, ':', ekok)
break
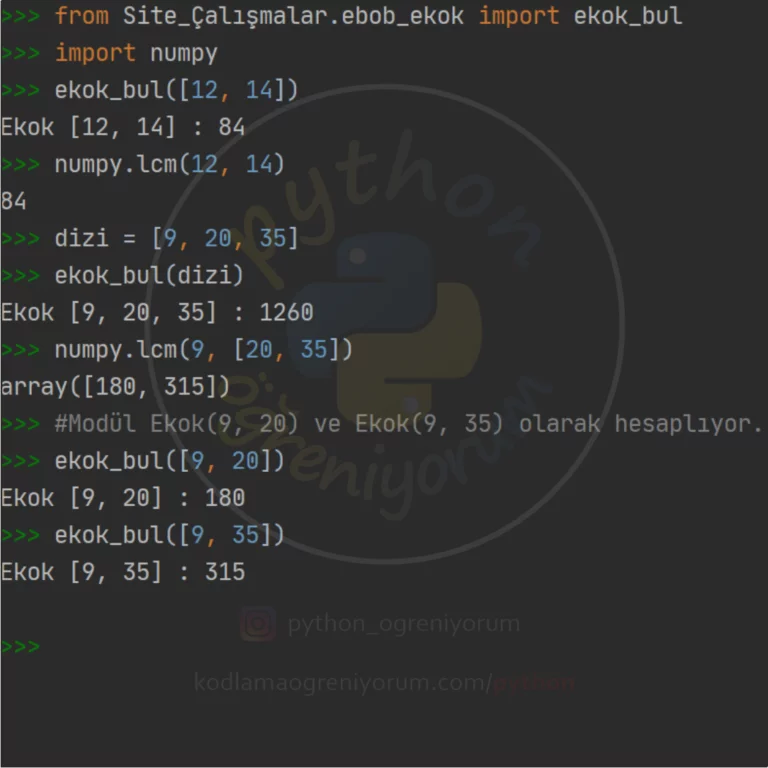
Python Modül Fonksiyonu: numpy.lcm()
Hesaplama yapmak istediğimiz sayıların en küçük ortak katı, maksimum o sayıların çarpımına eşittir. Örnek olarak: verilen iki sayı A ve B olmak üzere; A ve B’nin en küçük ortak katı maksimum “A x B”, verilen üç sayı A, B ve C olmak üzere; A, B ve C’nin en küçük ortak katı maksimum “A x B x C” olabilir. Bu yüzden, döngümüz elimizdeki dizinin çarpımına kadar gitmek zorundadır.(4. Satır) En küçük ortak kat olan sayı, dizideki bütün sayılara kalansız bölünür.(5.Satır) Ancak en küçük ortak kat olan sayının katları da dizideki sayılara kalansız bölüneceği için o sayının katlarına geçmeden döngüyü durdurmamız gerekir.(8.Satır)
EBOB:
1
2
3
4
5
6
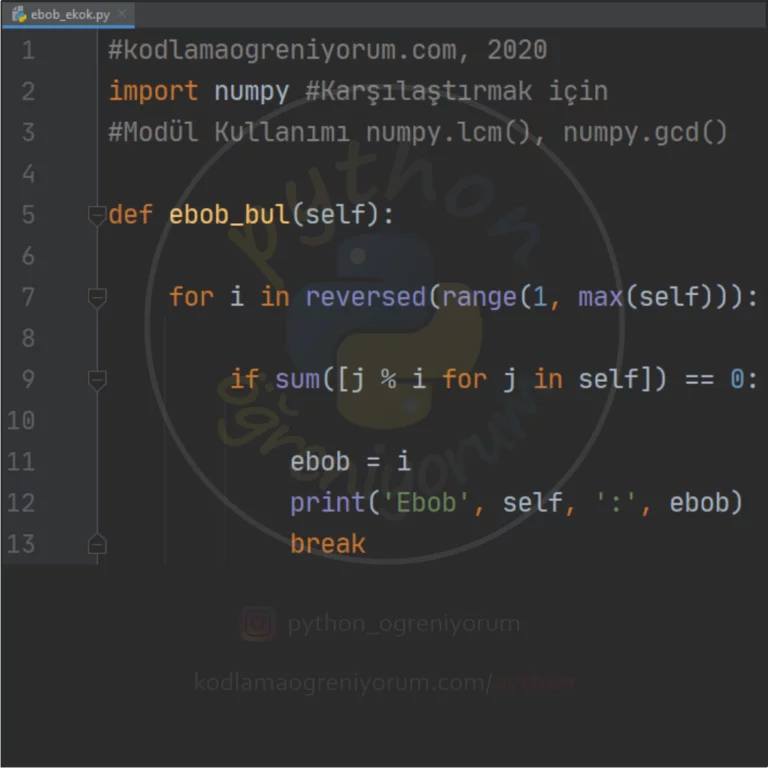
def ebob_bul(self):
for i in reversed(range(1, max(self))):
if sum([j % i for j in self]) == 0:
ebob = i
print('Ebob', self, ':', ebob)
break
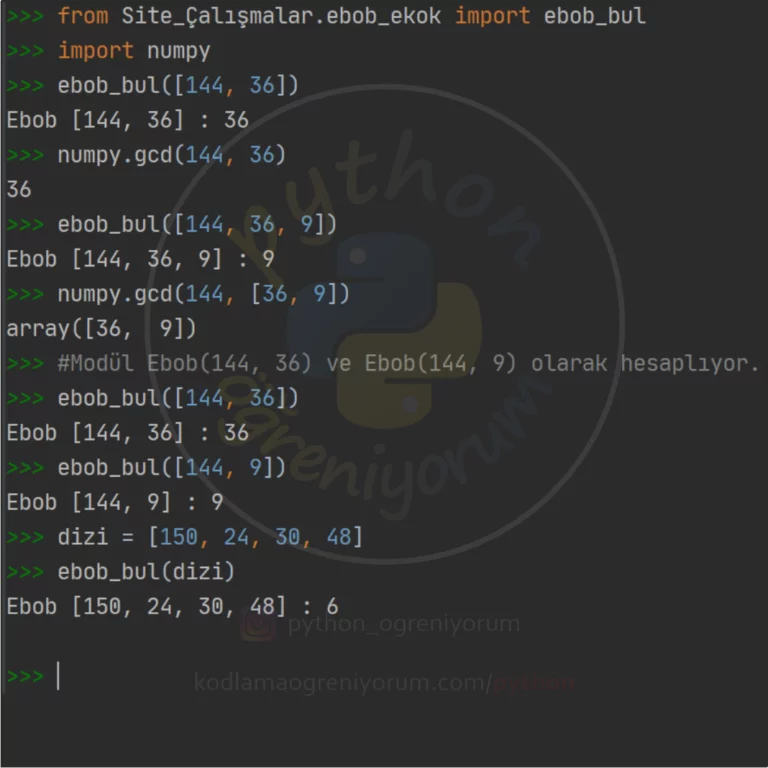
Python Modül Fonksiyonu: numpy.gcd()
En büyük ortak bölen sayıyı aradığımız için döngü iterasyonunun büyükten küçüğe doğru olması gerekiyor.(2.Satır) Birden fazla ortak bölen olabileceği için en büyük olanı bulduğumuzda döngüyü sonlandırmamız gerekiyor.(6.Satır)
Tek bir “script” dosyası altında toplayalım:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#kodlamaogreniyorum.com, 2020
import numpy #Karşılaştırmak için
#Modül Kullanımı numpy.lcm(), numpy.gcd()
def ekok_bul(self):
çarpım = 1
for i in self: çarpım *= i #Dizinin çarpımı
for i in range(1, çarpım+1):
if sum([i % j for j in self]) == 0:
ekok = i
print('Ekok', self, ':', ekok)
break
def ebob_bul(self):
for i in reversed(range(1, max(self))):
if sum([j % i for j in self]) == 0:
ebob = i
print('Ebob', self, ':', ebob)
break
ekok_bul([12, 14])
print('Modül Çıktısı:', numpy.lcm(12, 14))
dizi = [150, 24, 30, 48]
ebob_bul(dizi)
print('Modül Çıktısı:', numpy.gcd(150, [24, 30, 48]))
Bütün Python kodlarına Github sayfam aracılığı ile erişebilirsiniz. Github sayfamın linkine aşağıdan ulaşabilirsiniz. Görüşmek üzere!
Github: Github Python
Sitemize destek olmak isteyen sponsorlar için link: Patreon